这是我阅读《深入浅出统计学》一书的相关笔记和整理，这本书用了很多例子，读起来很好玩，在概念理解上让我很受启发。因此放在这里，以备日后查找。

1. 集中性和离散性、变异性度量

数值的集中性有三种度量方式，其一为均值μ，其二为众数，其三为中位数。当我们说平均数时，指代的不一定是其中哪一种。对于均值而言，其容易收到边缘值的影响，但最为常用。对于中位数而言，其弱化了这种趋势（按照顺序而非值的大小度量）。对于众数而言，其特征是：按照出现的频数进行比较。在遇到类别数据时可以使用，或者当数据可以分为多个组的时候使用。

因此，在数据非常对称，并且只表现出一种趋势的时候，一般使用均值（按值比较）。在数据有异常值的时候，使用中位数（按顺序比较）。在数据为分类或者可以分组的时候，使用众数（按出现频率比较）。

对于离散性度量，最简单的方法是全距，但是全距仅仅描述了数据的宽度，并没有描述数据在上下界限之间的分布形态。并且和均值一样，容易收到极端值影响。为了避免这种情况，我们可以按照顺序将数值分为四组，每组代表数值的四分之一，称之为四分位数。四分位距等于上四分位数（从上到下数第二个）减去下四分位数（从上到下数第三个）。没错，四分位距的重中点就是中位数。如果将数据分为100份，那么就有了百分位距。一般使用boxbar对四分位值进行表示。

对于变异性也要进行度量，我们可以使用方差表示变异性。为了单位一致性，一般使用标准差。标准差在数值分布图上表现最为明显，当我们说，一个数值位于距离均值1个标准差的范围内的时候，我们就是在说数值的标准分在均值±1个标准差范围内。

对于不同数据集中的数值进行比较，可以使用标准分，要点在于将各个不同的数据集转换成为标准正态分布，这样的话，对于每个数据集中的点，在转化为标准分数的情况下，可以相互比较。

2. 概率计算

2.1 使用韦恩图表示概率平面分布

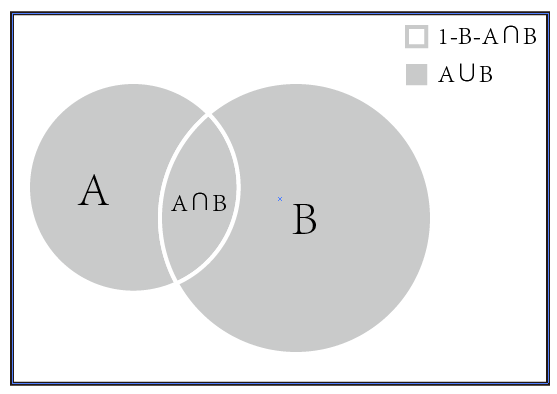
如上图所示，可以很方便的表示出A、B、A+B、A'、A∩B、A∪B的概率。对于没有交集的概率来说，称其为独立事件，对于有交集的概率来说，则表示其共同发生的概率。

P(A∪B) = P(A) + P(B) - P(A∩B)

此外，还有一种概率称之为条件概率，条件概率是一种在发生某事的基础上发生某事的概率，比如P(A:B)表示在发生B的基础上发生A的概率,由VNN图很容易得到：

P(A:B) = P(A∩B)/P(B)

为了方便，我们使用概率树来表示层次化的概率，也就是条件概率：

2.2 使用概率树表示时间序列概率

使用概率树很容易表示条件概率，比如：

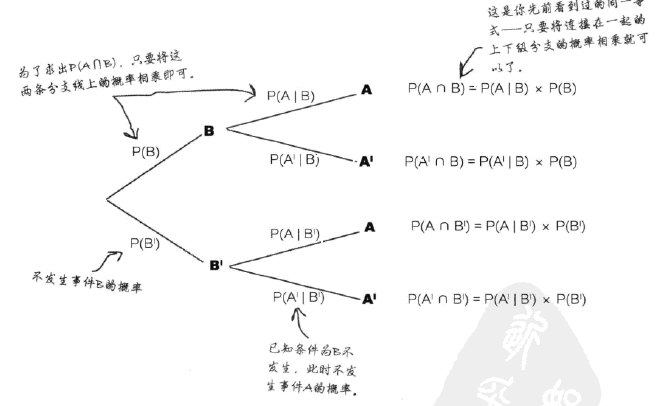
每个第二分支的概率都等于条件概率，其计算方法就是其标准定义——在VNN图很方便的可以描述—— P(A:B) = P(A∩B)/P(B)。在概率树上也很方便——只需要将第一个分支和第二个分支相乘即可。

2.3 贝叶斯定理

贝叶斯定理非常简单，就是两个公式进行的推导：

贝叶斯定理可以提供计算逆条件概率的方法，在你无法预知每种概率的情况下，它非常有用。

比如：一个游戏公司请志愿者玩游戏，80%人选择游戏1，20%人选择游戏2，在玩游戏1的人中，60%人觉得好玩，40%人觉得不好玩。在游戏2的人中，70%觉得好玩，30%觉得不好玩。

问：当随机挑选一名志愿者，问游戏是否好玩，她说好玩。那么，她在觉得游戏好玩时玩游戏2的可能性有多大？

3. 离散概率分布和期望

3.1 离散概率分布的期望和标准差

对于以上的x分布和其概率，我们可以求得其期望，期望定义如下，其代表了x最有可能出现的值。

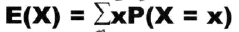
期望可以看作是一组数据表示集中性的统计量，那么方差可以看作是衡量离散性的指标，其定义如下：

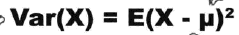
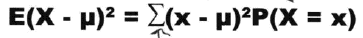
同样的，还有标准差：

3.2 离散概率分布的变换

线性变换的期望和方差：

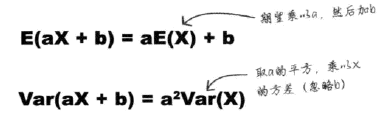
独立观测值的期望和方差：

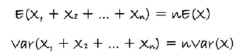
线性变换后加减的期望和方差：

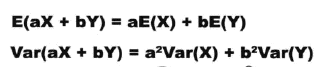
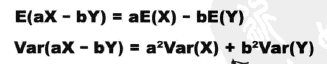
4. 排列组合

排列：从n个样本中拿出r个，其方式有：

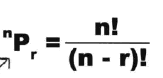
组合：从n个样本中拿出r个，不要求排列，其方式有：

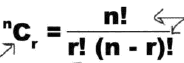
其中排列指的是从一个群体中选取一个对象，考虑每种顺序组合。组合则只是从一个群体中选取几个对象，不要求对象的排列，因此，相比较排列要除以那些对对象进行排列的个数。

5. 常用离散概率分布模型

对于离散的数据，常见的分布形态有几何分布、二项分布以及泊松分布。它们都是概率分布的特殊类型。在之前章节中，我们知道计算和利用概率分布需要知道每种条件，以及每种条件下对应的P(X=x)概率。但是，对于一些特殊的概率分布，如果其特征符合这三种，我们就可以以很快的速度计算其概率、期望和方差。

5.1 几何分布

几何分布的条件是：进行一系列相互独立的实验，每次实验都有两种可能，其中单次成功的概率始终固定，为p。

几何分布适用于已知概率p(probability)而未知次数n的情况。我们使用这种分布一般感兴趣的问题是：为了取得第一次成功需要多少次试验。

对于概率树进行遍历可以看到，概率p在计算的时候重复了r-1次，而（1-p）则只有1次，因此有：

X ~ Geo(p)

P(X=r) = p · q^(r-1)

其中r表示数值为r时的情况，p表示成功的概率，q表示失败的概率，
P(X=r)表示X等于数值r的概率（取得第一次成功的概率）。

P(X>r) = q^(r-1)

需要试验r次以上才能取得第一次成功的概率

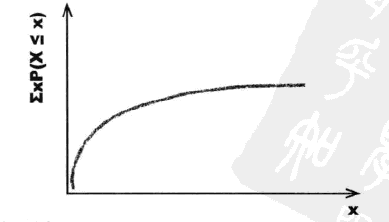
P(X<=r) = 1 - q^r

需要试验r次或者不到r次即可取得第一次成功的概率

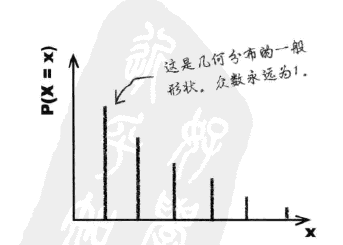
几何分布的图像是一个x轴为r，y轴为P的递减曲线，其一个特点是：任何几何分布的众数都永远是1。因为可能性最大的情况始终是：仅尝试一次即可获得成功。

几何分布的期望值，也就是说，我们期望在X=某个r的情况下最有可能获得成功的这个值为：

E(X) = 1/p

期望的变化如下：

这意味着，如果某事服从几何分布，并且其概率为0.2，那么尝试5次后期望获得第一次的成功。

Var(X) = q/p^2

方差的变化如下：

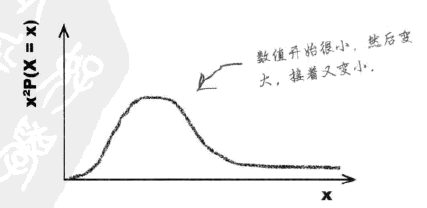
上述例子中的期望变异性为0.8/0.04=20,提醒：Var(X) = E(X^2) - E(X)^2

5.2 二项分布

将几何分布推广到一个特殊情况：当事件独立并且每个事件有两种互斥的结果，并且每个事件相互独立的情况下，已知总的次数n，问r个事件成功的概率。注意到这里的区别，对于几何分布，我们只需要在所有事件中有一个事件成功即可结束，而在二项分布中，我们需要遍历n个事件，并且求得其中r个事件成功的概率。

联系到排列和组合，从n个事件中取出r个事件的情况有C(n,r)种。

于是很容易就可以得到：

X ~ B(n,p)

P(X=r) = C(n,r) · p^(r)· q^(n-r)

其中C(n,r)等于 n!/((n-r)!·r!)，n为总的次数，r为成功的次数之和，
p为成功的概率，q为失败的概率，P为n次中有r次成功的概率。

期望和方差如下：

E(X) = np

对于一次的实验，E(X) = p，由于所有实验独立，
因此E(X)就等于所有的独立实验之和。下同。当r=np附近，有众数出现。

Var(X) = npq

5.3 泊松分布

泊松分布适用于以下情况：不存在一系列的实验，反而，我们已经从历史数据中知道了故障发生的几率（发生率而不是概率，使用λ表示），并且故障是随机发生的（两个条件）。

此种情况的问题在于，我们知道平均故障次数，但是实际次数却是不固定的。有可能不出现故障（概率低），也有可能出现各种故障（概率低），那么，如何求解出现某一次数的概率呢？

X ~ Po(λ)

P(X=r) = e^(-λ) · λ^r / r!

E(X) = λ

这个很容易理解，因为其实泊松分布就是已知期望求概率

Var(X) = λ

泊松分布的形状如下：

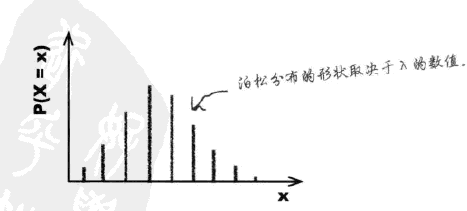
泊松分布有一系列好玩的特性，比如，对于事件X和Y，有：

P(X+Y) = P(X) + P(Y)

E(X+Y) = E(X) + E(Y)

如果： X ~ Po(λ1) Y ~ Po(λ2) 那么：

X + Y ~ Po(λ1+λ2)

此外，对于二项分布，如果np ≈ npq（二项分布的期望等于方差，在泊松分布中是必要的），那么可以近似看作泊松分布。其中λ可以使用np来代替。也就是：

X ~ Po(np) 近似于 X ~ B(n,p)

举个例子

1、一辆公共汽车平均每15分钟停一站，在15分钟内不出现公共汽车的概率有多大？

15分钟内出现汽车的情况有0和1这两种发生率，因此符合λ(1)的分布，求得P(X=0)的值为0.368。

2、对于上述问题，在5分钟内出现汽车的概率有多大？

解答1：

从15分钟内抽取任意连续的5分钟，一共有三种情况，符合X~B(3,0.368)，P(X=1) = C(3,1)*0.368^(1)· 0.632^(2) = 0.882

一个可能的问题是，这三种情况是否独立？

解答2：

表格表示5分钟内的x和p的可能情况，其中x=0的概率为10/15=2/3，x=1的概率为1/3。那么，E(X) = 1/3,因此符合λ(0.33)的泊松分布，求解得：

P(X=0) = 2.72**(-0.33) * (0.33)**0 / 0! = 0.718

6. 连续概率分布

6.1 正态分布概要

不同的数据类型影响求解概率的方法。对于离散概率分布来说，我们知道对应的x取值和其p值，然后可以求得E和σ。但是对于连续概率分布来讲，我们没有x和p值表格，反之，我们知道“概率密度曲线”，这里的概率密度曲线近似于x值-p值的函数，而一段范围的概率，我们可以使用求密度曲线和x轴包裹的面积来计算。

连续数据的理想模型是“正态分布模型”，这种模型的图像类似钟形曲线，两段低，中间高，并且这两端的概率永远近似等于0。正态分布的均值和中数位于中央，具有最大概率密度。正态分布通过两个参数进行定义，μ和σ^2，写作

X ~ N(μ,σ^2)

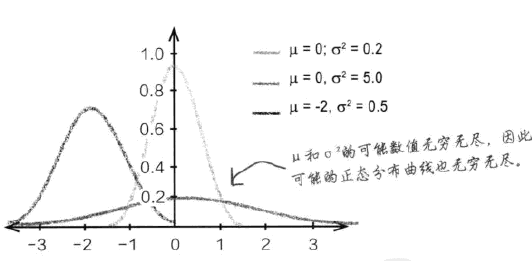
连续曲线密度的分布随着μ和Var的变化而变化，Var越大，那么钟形开口就越大，如果μ越大，那么曲线就向右进行偏移。对于一段范围的概率进行计算，通常要求这段范围内的曲线和x轴包裹的面积大小，这就是其概率，一般需要用到积分。通常需要对非标准的正态分布进行标准化以求解其阈下面积，这是因为，通常课本上给出的正态分布表只是对应均值为0，方差为1的正态分布而言的。

对于 X ~ N(μ,σ^2)，我们将其标准化后发生了什么？

首先，向左移动u个单位，得到

X - μ ~ N(0,σ^2)

然后，线性变换σ个单位，得到：

 (X - μ) / σ ~ N(0/σ,σ^2/σ^2) ~ N(0,1)

这样的话，我们就可以说，对于 Z = (X - μ)/σ 而言，其服从标准正态分布，因此可以用标准正态分布的公式求算概率。经过标准化变化之后的整个区间并没有增大或者缩小，一切比例都保持相同，由于代表概率的是面积，因此概率也保持不变。

6.2 正态分布的运算

6.2.1 正态分布 ± 正态分布

对于两个不同均值和方差的正态分布，我们可以将其合起来进行计算。由于在之前我们已经知道，对于独立事件，

E(X±Y) = E(X)±E(Y)

Var(X±Y) = Var(X) + Var(Y)

所以，如果 X ~ N(μ1,σ1^2)， Y ~ N(μ2,σ2^2)，那么：

X ± Y ~ N ( μ1±μ2 , σ1^2+σ2^2 )

6.2.2 正态分布的线性变换

同上：

所以，如果 X ~ N(μ1,σ1^2)，由于：

E(aX + b) = a·E(X) + b 

Var(aX + b) = a^2·Var(X)

那么：

aX + b  ~ N ( a·μ+b , a^2·σ^2 )

6.2.3 独立观察的正态分布之和

同上，如果X1...Xn为独立观察结果，那么：

(X1 + X2 + ... + Xn) ~ N(n·μ, n·σ^2 )

6.3 使用正态分布进行替代计算

我们可以将满足一定条件的离散分布使用正态连续分布来代替计算。但是一个问题是，相比较连续分布，离散分布在计算的时候需要进行连续性修正。对于任何分布都需要进行修正。

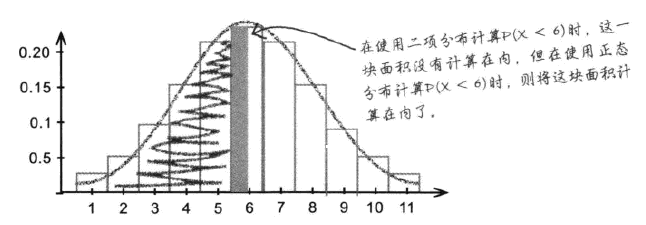
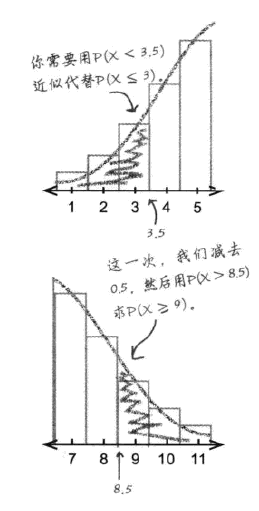
如上图所示，对于离散分布，在对于某个分界进行计算的时候，我们所求的面积是其高度乘以变量宽度。而在连续分布中，我们计算的就变成了精确到某一刻度的积分。这造成了误差。因此，对于≤型概率的连续性替换，我们需要在离散分界值上加上变量宽度的一半。，对于≥型连续变量替换，我们需要在离散分界值上减去变量宽度的一半。其含义为，当我们需要使用连续（精度更高的方法）进行计算的时候，我们需要矫正传入参数的误差——这个参数本来是为非连续分布服务的。

6.3.1 代替泊松分布

对于泊松分布，如果在 λ > 15 的情况下，我们可以近似认为其分布接近于正态分布。那么，就可以使用正态分布进行替代计算。

X ~ Po(λ) 当 λ > 15 的时候，近似于 X ~ N(λ,λ).

注：泊松分布的均值和方差都是λ.

6.3.2 代替二项分布

对于二项分布，如果在 np > 5 或者 nq > 5的情况下，我们可以近似认为其分布接近于正态分布。实际上，我们的定义为 n>50,p>0.1的时候，可以使用正态分布代替计算。

X ~ B(n,p) 近似于 X ~ N(np,npq) 当 n>50, p>0.1

不论是使用二项分布还是泊松分布替代——正态分布，都需要进行连续性修正，不管它们本身是否很好的拟合了所有的数据。

6.4 一点思考

对于一个班级所有学生的成绩分布可以近似看作正态分布。那么，其平均值和方差反映了这个班学生成绩的离散程度。将其标准化后，我们所求的排名、概率都没有改变。我们注意到，在标准化的过程中，我们排除了均值和方差的影响，因为标准化强制让均值等于0，方差等于1，这样我们就可以很方便的和不同的其他分布进行转换后的标准分布进行比较。

7. 样本抽取和分布

我们之前所有的概率都是基于总体而言的。但是，实际生活中，我们无法穷尽所有的总体，或者这样的成本太高或者根本不足以成行。因此，采用少部分单位代替总体，我们称其为样本。对样本而非总体进行统计检验，就轻松很多。问题的关键在于，样本如何代表总体？

7.1 抽样步骤

设计一个好的样本需要以下三个步骤：

• 确定目标总体。目标总体很关键，对于不同的目的，我们的总体几乎都不同。并且，我们需要总体尽可能的精确，这样更容易获得尽可能代表总体的样本。

• 确定抽样单位。抽样单位指的是，我们需要抽样的元素的范畴，比如抽取一盒口香糖还是抽取一只口香糖。

• 确定抽样空间。在确定抽样的最小单位和目标总体后，我们需要将总体按照最小抽样单位划分成为可用于抽样的抽样空间。这很难，因为我们有时候面对的是流动的群体，或者难以对总体进行合适的分割。

总而言之，抽样必须按照上述步骤来进行，这里的每一步都有可能影响样本代表总体的能力。

7.2 选择样本

我们有以下几种方法选取样本：

• 简单随机抽样，其中包括重复抽样和不重复抽样。

• 分层抽样。分层指的是按照某一特征将个体分到不同的层中，然后对每层进行抽取，比如按照男女分层，然后对每层抽取一定的比例。

• 整群抽样。整群抽样和分层不同的是，整群需要将不同的个体划分到一个群中，群和群之间类似。然后对群进行随机抽样。分层的不同曾代表了具有不同特征的相似个体，这和整群抽样中的群不同。

• 系统抽样。系统的按照某一顺序抽样，比如尾号为5的，这种方法不适合从有明显特征和循环的排列中抽取。

7.3 点估计量代替总体参数

7.3.1 总体方差和均值的点估计

样本均值和总体均值的估计

对于样本的统计量，如何和总体的统计量之间建立关系呢？

对于均值，总体的均值使用μ表示，而μ^则表示对于总体均值的点估计。对于样本而言，其也有一个均值，叫做x拔(x加上一个上档线)。我们估计的总体均值等于x拔，而总体均值和总体均值的点估计值之间的相等与否，就看我们样本是否能够代表总体了。

大概来说，就是这样：

样本方差和总体方差的估计

对于总体方差的估计量，采用：

同样的，我们有总体方差(σ^2)、总体方差的点估计((σ^)^2)、样本方差(s^2)三个变量。需要注意，样本方差计算时取n，但是样本方差作为总体方差的估计量的时候计算时取n-1。

7.3.2 样本比例的抽样分布

由样本估计总体

如果有两种球，白色和红色，共100只。现在抽取一个n=10的样本，其中白色7只，红色3只，问总体的白色球比例如何？

如果用X表示总体中白色球的数量，那么X符合二项分布，参数为n=100，p=？。总体白色球的概率的点估计就是样本白色球的比例，其中样本白色球比例为白色球数量和总的球数量之比。

由总体估计样本

如果说，已知100个球中间有红色球25%，那么抽10个球，抽中至少40%的红色球的样本的概率为多少？

比例的抽样分布中，对于球的总体满足二项分布，其中n=100，p=0.25，X~B(n,p)。

对于样本而言，使用X表示样本中红色球的数目，那么X~B(n,p)，其中n=10，p=0.25，这是由于总体分布的特性得到的。但是，当我们真的进行抽取的话，从样本中抽取红色球的比率为：Ps=X/n。利用所有的Ps可以得到样本的抽样分布。

E(Ps) = E(X/n) = E(X)/n = np/n = p

Var(Ps) = Var(X/n) = Var(X)/ n^2 = pq/n

当n很大(n>30)的时候，也就是样本越来越接近总体的时候:

Ps~N(p,pq/n)

上述问题为：Ps~N(0.25,0.25*0.75/10) 求P(Ps≥0.4)

我们知道，离散转连续一般都需要进行连续性修正，对于X进行±(1/2)即可修正，对于Ps而言，修正量就是：±(1/2)/n = ±(1/2n)。随着n的增大，连续性修正就变得很小，有时候会直接忽略。

7.3.3 样本均值的抽样分布

为什么我们需要样本均值的抽样分布？一个例子是：对于糖果，每袋含有的数目是不定的，我们知道总体每袋中的均值和方差，现在进行抽样，我们需要计算样本中每袋数量平均为某个值的概率，这个时候，就需要使用样本均值的分布。

假设每袋含有的数量为X，对于每个单独的样本，其E(X)=μ，Var(X)=σ^2，其中μ和σ^2都是总体的均值和方差。对于样本平均值来说，x拔等于(x1+x2+...+xn)/n，则：

E(X拔) = (E(X1)+E(X2)+E(X3)+...)/n = μ

Var(X拔) = σ^2/n

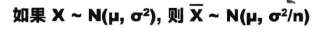
同样的，当n很大的时候，可以近似用正态分布代替。这里的n需要大于30.

需要澄清一个问题，也就是，样本均值的分布和样本的分布的区别，如果说，问题是：我们需要计算样本中每袋数量为某个值的概率，也就是X的概率，那么使用样本就行。但我们的问题是需要计算样本中所有个体的X的平均值的概率，这就需要对X拔进行分布的估计和计算。

7.3.4 中心极限定理

中心极限定理指的是，对于任何非正太总体X，从其中取出一个样本，这个样本很大，则X拔的分布近似为正态分布。如果总体的均值和方差为μ和σ^2，并且n很大，那么：

中心极限定理对于总体为二项分布、泊松分布也有很大的用处，在之前我们知道对于总体而言，二项分布服从：

X ~ B(n,p) 近似于 X ~ N(np,npq) 当 n>50, p>0.1

那么，X的均值的分布近似于：

X拔 ~ N(np,pq)

对于泊松分布而言，

X ~ Po(λ) 当 λ > 15 的时候，近似于 X ~ N(λ,λ).

那么，X的均值的分布近似于：

X拔 ~ N(λ,λ/n)

需要注意，中心极限定理不需要进行连续性修正。

7.4 无偏估计

无偏估计指的是，从总体中进行抽样，抽取的样本的期望等于总体参数的真值。

点估计量和均值、方差、比例的抽样分布之间的关系如下：

8. 置信区间的构建

8.1 X拔近似服从正态分布

我们现在有了从总体中抽取的样本，有了样本的分布。现在我们可以使用一个由样本得来的统计量来很好的概括总体，其被称之为置信区间，这种方法考虑到了样本分布的不确定性。可以将置信区间看作是样本分布的一个数学抽象。

问题：如果我们从包含100颗糖的样本中得出其口味持续时间均值的点估计量为62.7分钟，总体方差的点估计量为25分钟。那么，我们如何描述，糖的口味持续平均时间？如果我们说其持续时间为62.7，那么必然是不准确的，因为任何人进行试验都会发现其持续时间或多或少，因此，我们需要将样本均值的分布抽象化，计算一个持续时间的范围来代替持续时间的点估计量（也是样本均值的期望值）。

这个问题非常简单，当我们确定需要抽样的是样本均值，我们就可以对样本均值的分布进行计算：

对于样本均值的分布而言，有：

E(X拔) = (E(X1)+E(X2)+E(X3)+...)/n = μ

Var(X拔) = σ^2/n

所以上述问题可以表述为：

X拔 ~ N(μ,0.25) 

由于总体方差未知，所以使用s^2来代替σ^2。然后我们将其分布标准化，得到：

(X拔 - μ)/((s^2/n)^0.5) 的95%置信区间在(0.025,0.95)

因此就可以求得μ的置信区间。

当然，我们有一些简单算法，如下图所示：

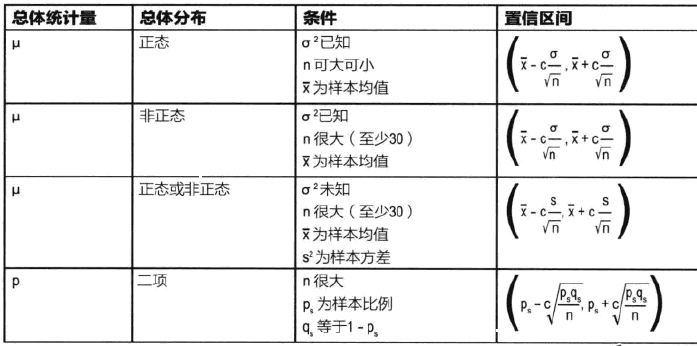
对于置信水平和c值而言，90%的置信水平对应c为1.64，95%的置信水平对应c为1.96，99%的置信水平对应c为2.58。

8.2 X拔服从t分布

对于抽样样本过少(n<30)的情况，X拔的分布不一定为正太分布，这时候就需要使用t分布。t分布有一个参数称之为v，v=n-1，其代表自由度。一个被检验的统计量符合t分布且自由度为v的写法为：

T ~ t(v)

而T的计算方法和之前的X拔一样，T = (X拔 - μ)/((s^2/n)^0.5)。区别是，对于t分布，默认使用样本方差代替总体方差，因此直接使用s而不是σ。t分布概率表需要自由度和尾部概率值，就可以求得t(v)值，之后代入求μ的置信区间即可。

对于t分布的置信区间的一个简单算法如下：

8.3 一点思考

糖果公司发现他们的装糖机出了一点问题。他们抽取了30台机器作为样本，发现故障次数均值为15，请问每月故障次数构建一个99%的置信区间。

这个题容易出错的点在于：把泊松分布转换为正态分布后继续由中心极限定理转换为X拔的样本分布。其实后者是不必要的，因为泊松分布本身就是由样本得来的，或者你可以叫这个分布为样本均值的泊松分布，所以在这里不存在样本和总体的关系，因此泊松分布的期望和方差均为λ，代入计算即可。

9. 假设检验

在上一节，我们使用样本的置信区间来概括从总体中抽样的分布情况。在本节中，我们换一种方式探讨这个问题——对于一个断言，我们有多少的确信能够说这个断言是错误的？

需要注意，这里的断言针对的是样本，比如：我们断言一种药物的疾病治愈率为90%，那么很显然，对于抽样n=100的样本，我们期望有90个人被治愈。那么，在实际中，我们有82个人被成功治愈，在这种情况下，我们有多大的把握说其断言正确呢？

我们使用假设检验的方法来处理这个问题。

首先提出原假设：H0：p=90%

接着我们要假定原假设不成立的基础上提出备择假设，备选的假设不一定要和原假设互斥。比如：H1：p<90%

之后我们假定原假设正确，那么对于被治愈的个体，满足X~B(100,0.9)的正态分布(二项分布近似)——X~N(90,9)。在这种情况下，我们有了一个抽样的分布，接下来，就要检验P(X=82)的概率。

首先将其分布标准化，得到 z = (82-90)/3 = -2.67, p = 0.0038

对于样本分布而言，单尾95%的置信区间对应的p值为0.05,所以z值落在了拒绝域内，所以，原假设无效，治愈概率低于90%。

假设检验不一定要使用正态分布，而是要根据已知的条件来进行计算。比如我们可能用到t分布、二项分布或者泊松分布。

此外，假设检验还可能遇到错误。我们将错误的拒绝原假设的错误称之为第一类错误，犯第一类错误的概率为显著性水平α。将错误的接受原假设的错误称之为第二类错误，犯这种错误的概率为β。第二类错误的求解需要备择假设为一确定数值，比如治愈率为80%作为备选假设。

根据α水平逆向标准化正态分布求出当X大于或者小于多少的时候我们会接受原假设。之后，根据备选假设的p值和样本总体n值构造一个分布，求解我们接受原假设的概率，这就是第二类错误β的概率。

假设检验有一定的功效，只有求得第二类错误的概率，才可以求功效。功效=1-β。

需要注意，对于假设检验而言，我们不需要使用X拔的分布而直接使用X的分布的原因是，我们知道了一个总体的断言，这个断言对于无偏样本来说就是一个单纯的数值，我们需要检验在我们自己抽样的样本中，这个数值偏离样本期望的程度。这里的计算和X的均值毫无关系，而是和X的分布有关。而在置信区间章节中，使用X拔的目的仅仅是因为我们关注的重点是X的均值，所以对这个均值进行估计就要使用样本均值的分布来进行计算。

10. Х2分布

10.1 拟合性检验

卡方分布被用于两种情况，其一为拟合度检验，其二为独立性检验。

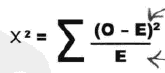
如上所示，O表示观测值，E表示期望值，卡方大到一定程度之后，我们认为其超过了合理偶然性的范围。

卡方分布有一个参数称之为自由度，一般情况下，当df等于1或者2的时候，卡方分布为一条如下所示的曲线，当df大于2的时候，曲线变为一种中间凸起，两边凹陷的钟形曲线，随着自由度越来越大，其分布越接近正态分布。

对于特定参数v的卡方分布和统计检验量X2，可以写作：

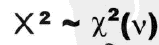
自由度df或者v等于独立观测的组数减去受到的限制数目，对于观察和期望而言，其综合必须相同，那么这意味着我们计算时受到1个限制。

卡方分布只能够使用右尾检验，在概率表找到对应自由度和显著性水平的临界水平，和检验统计量X2进行比较，如果检验统计量大于临界水平，则检验统计量位于拒绝域内。

卡方拟合度检验对于很多概率分布都有效，比如：

10.2 独立性检验

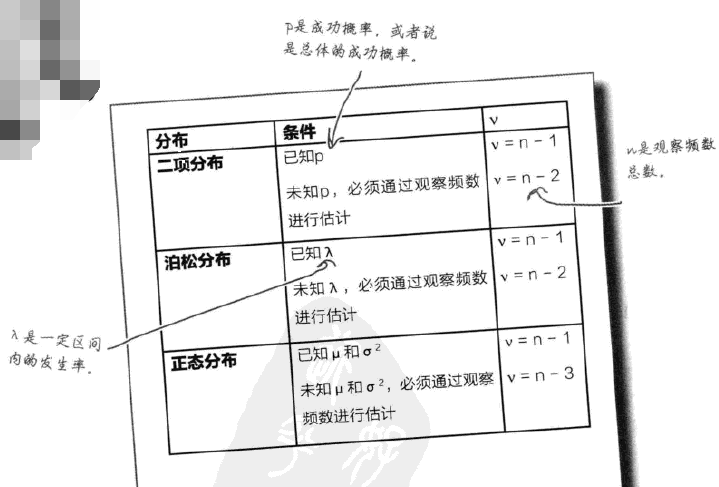
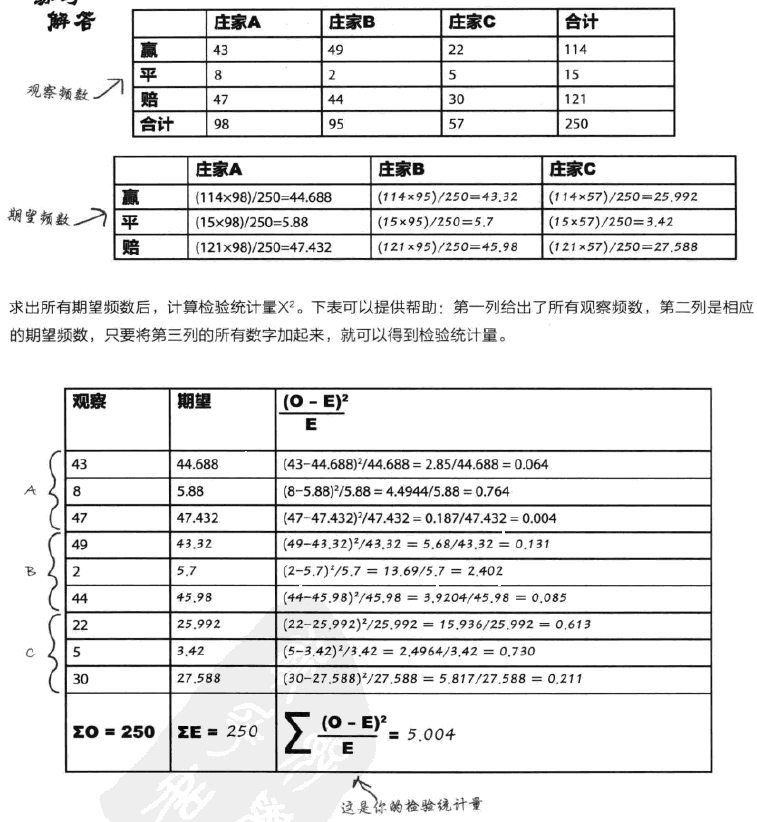
独立性检验和拟合检验非常类似，区别是自由度需要经过一定的计算，一般来说，自由度表示总的独立变量减去受限个数，对于行列式h×k来说，df一般等于(h-1)×(k-1)。此外，需要根据实际数据求得期望数据，这很简单，算好比例就行了，比如对于某一行列值来说，只需要计算这个值对应的行总和值乘以列总和值然后除以总的行列数值，就是期望，使用频数和期望求得所有情况下的卡方，然后代入其分布计算各项目（行和列）之间是否独立。

————————————————————————————

更新日志

2018-04-06 更新二项分布、泊松分布、几何分布部分。

2018-04-07 更新正态分布部分、抽样部分。

2018-04-08 更新置信区间、假设检验、卡方分布部分，补充连续和离散度量、排列组合、离散分布部分。